PID Terminology 2

Introduction to PID Terminology

PID Terminology is essential to understanding how PID works. For this reason, we’ll go through various terms you will see when reading about PID. In short, PID itself stands for Proportional, Integral, and Derivative. Basically, the purpose of PID is to hold analog values at a certain setpoint. For example, if you have a heating process, the PID will provide the right amount of output to achieve the correct temperature. Other examples include flow rates, pressure, and tank levels.

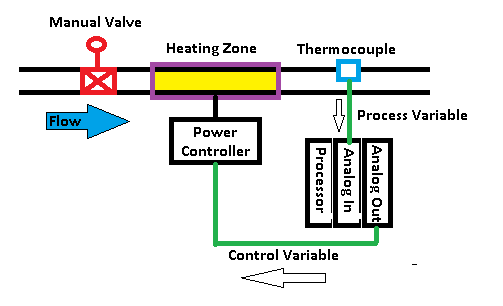
Main Variables of PID Terminology

Setpoint — This is our target for the feedback. Generally, this will be the temperature, pressure, flow rate, or level that you desire.

Process Variable — This is feedback from your system. Basically, this is the value from a sensor such as a thermocouple, or pressure transducer.

Error — This is the difference between the Setpoint, and the Process Variable. If the Process Variable is below the setpoint, error will be positive or negative depending on the type of control action you choose.

Control Variable — This is the amount of output the PID sends to your field device. This is typically in the form of an analog signal. Whenever the PID settings are correct, the control variable provides just the right amount of output to achieve the setpoint that you desire.

Deadband — This is an area near the setpoint where there is no control action. You might use this to prevent over cycling of a valve. You will also see Zero Crossing deadband. In this case, control action stays active until the process variable crosses zero. In other words, once you are outside of the deadband, you will have controller action until the process variable crosses zero.

Feed Forward — You can also think of this as BIAS. Use Feed Forward to anticipate a change before it happens. For example, let’s say you will draw more water from a tank. As soon as you open the valve, you can send the percent of change to the tank level controller. The control variable immediately offsets due to your demand. After that, your regular PID equation works to remain at the setpoint.

Detailed PID Terminology

Proportional Gain / Band

Proportional — This gain setting determines the controller’s output based on error. For example, if the gain settings is 2, and the error changes by 5, the effect on the output is a value of 10. It’s important to realize that some controllers have different units.

You could also see the Proportional setting labeled as bandwidth. In this case, a bandwidth of 100% is the same as a gain of 1. A bandwidth of 50% represents a gain of 2, and so on. This is because a gain of 2 only starts to reduce power in 50% of the band. In other words, if it’s a heating process, you will have 100% power until the error drops below 50%. Likewise, if the gain is 4, then you will have 100% power until the error drops below 25%. If you set the gain too high (or band too low), the loop becomes unstable. This will cause continuous oscillations in your process variable.

Integral (or Reset)

Integral — Integral picks up where proportional falls short. As long as an error is still present, integral will keep changing the controller’s output. For example, let’s say we are in a position based loop using the independent equation. After the action of proportional gain, we still have an error of 10%. If gain is set to 1, then we have 10% output based on proportional gain only.

Think of a heating process. As a thought experiment, assume for now that the error does not change. This assumption will help us to think how integral action works. At this point, we change the integral setting to .1 repeats per second. Obviously, after 10 seconds, we would have 1 repeat. Since the error was 10%, then we add 10% more to the output in these 10 seconds. Therefore, the total output would be 20%. After 10 more seconds, if the error has not changed, we add another 10%. Hence, after 20 seconds, your total output is 30%, and so on.

It’s important to realize that in a real application, the error should decrease as we add output. When the error decreases, the Integral action adds less output. Integral action would not reduce the output. It simply has less to add because there is less error.

Always pay attention to the units on your controller. You will see the units as repeats per second, seconds per repeat, minutes per repeat, etc.

Derivative Action

We use Derivative to anticipate that we need more output. Once again, imagine a heating process. The temperature begins to drop fast. At first, there is not much error, so we do not have much proportional action. Not a lot of time has passed, so once again, there is not much integral action. We do, however, have a huge rate of change of error. The derivate will see a large slope in error, and predict what the error will be in the future. The derivative control will add an output accordingly.

This setting is typically in minutes. The larger the number, the larger the derivative action will be for a given slope in error. At the same time, the larger the slope of error, the more derivative action you will have as well. Most loops do not contain derivative action. This is especially true if the process variable is noisy.

Another key point is that derivative action will act both ways. In a heating process, it would add to the output when the process variable drops. Furthermore, it will decrease the output as the process variable increases.

Control Action

Forward Acting — We calculate the error as Process Variable – Setpoint. Therefore, if the process variable is below the setpoint, output decreases because the error is negative.

Reverse Acting — We calculate the error as Setpoint – Process Variable. In this case, if the process variable is below the setpoint, the error is positive.

PID Terminology for Equations

Dependent — We calculate the total output of the Control Variable using the Dependent PID equation. A change in controller gain affects integral, and derivative as well.

Independent — Use this equation to calculate proportional, integral, and derivative separately. The sum of each component will be your output.

Types of PID

Position Based — Proportional, integral, and Derivative will be calculated based on their current values in time. Calculations are based on current error. For example, if we reset the controller, and set gain to 1, and error is 10, then the output will be 10%. At this point, we change the gain to 2. At this point, the output immediately jumps to 20%.

Velocity Based — In this case, our calculations are according to the change in error. For example, if we reset the controller, and set gain to 1, and error is 10, then the error will be 10%. At this point, we change the gain to 2, the output does not immediately change. After that, if the error changes by 1%, the output changes by 2%.

Types of Processes

Self Regulating — A self regulating process has a form of natural stability for a given control variable. For example, consider a temperature control system. If you increase the output in manual mode, the temperature will stabilize at a higher temperature. This is due to the non-linear nature of the process. In other words, when the temperature is higher, you will have more losses. These losses include ambient losses, losses due to load, and electrical losses at higher temperatures. Other self-regulating processes include flow, and pressure. In manual mode, a change in gain results in a change in the CV. However, when you return the CV back to it’s original value, the PV also returns to it’s original value. It’s possible to use tuning methods on self-regulating processes that require temporary open loop control.

Non-Self Regulating — Non-Self regulating processes are those in which an increase (or decrease) in the control variable sends the process variable perpetually in one direction. A good example of a non-self regulating process is a tank which has no losses. If the inflow is slightly greater than the outflow, the tank level will continuously increase. In this case, the loop must be closed in order to maintain a particular level. These are integrating processes. In manual, when you change the CV, and put it back to the original value, the process variable will not return to it’s previous level. Instead, the process variable simply levels out.

For more information on PID, take a look at the Ladder Logic, or Function Block posts!

— Ricky Bryce