Introduction to Kenbak-1 Multiplication
Kenbak-1 Multiplication involves creating loops. Being designed in 1971, the Kenbak-1 has a limited instruction set. That limited instruction set presents some good challenges. These challenges force us not only to understand the Kenbak-1 itself, but also understand more about mathematics.
There is no direct instruction in the processor for performing multiplication. We perform multiplication by adding the multiplicand over and over by the number of times defined by the multiplier. In this post, I’ll demonstrate this method of multiplication in the Kenbak-1. It’s a bit crude, but remember this was back in 1971. The Kenbak-1 did not even have a processor as we know them today.
In this section we’ll develop a simple program. The program has no other purpose than to multiply two small numbers together and display this to the user. The user will enter these two values into addresses 020 and 021.
Obviously, when using only 8 bits, the result must be below 377 octal (255 decimal). We’ll discuss how to deal with larger numbers in a future post by using the carry bit.
If you haven’t done so yet, I would encourage you to read the post on the Kenbak-1 OPCODES to understand how to build the instructions below. Additionally, you will probably want to print out some of the Kenbak-1 Programming Worksheets.
Initialize the Registers
First, we’ll start this program by initializing the A, B, and X registers. We’ll also set the program counter (PC) to start in memory cell #4. Remember, the location of the A register is at 000. The B register is at 001, and the X register is at 002. The Kenbak-1’s program counter resides at address 003. This keeps track of the next memory cell as the program executes.
I’ll be using the Kenbak-1 Web emulator for this, but you can enter the program in an Kenbakuino as well. At the end of this post, I’ll list an octal dump that you can send to the Kenbakuino.
INIT
000: 000 000 000 004 Create the Loop for Kenbak-1 Multiplication
Since this is a very small project, we’ll only have a single loop to execute. After that, we’ll send the results of our multiply to the display. Keep in mind, though that all of the values for the Kenbak-1 are in OCTAL. You can verify the results with a programming calculator. Just be sure your programming calculator is set to OCTAL as well.
At memory cell 004, we load the X register with the value of 021. This will be the number of times that our loop executes. At memory cell 006, we add the value of cell 020 to the accumulator (“A” Regsiter).
We need to keep track of the number of times the loop executes, so we decrement the X register in cell 010. Every time the loop executes, X will decrement.
In memory cell 012, we check the value of X. As long as X is above zero, we execute the loop again. Once X drops to zero, we know that the “A” register contains our answer.
In Line 014, and 016, we store this A register both to cell 022, and to the display.
004: 224 021 LDX 101 (LOAD X WITH [021])
006: 004 020 ADD A 100 (ADD [020] TO A)
010: 213 001 SUB X 001
012: 247 006 JPD 006 ON X>0
014: 034 022 STA 022
016: 034 200
020: 010
021: 010
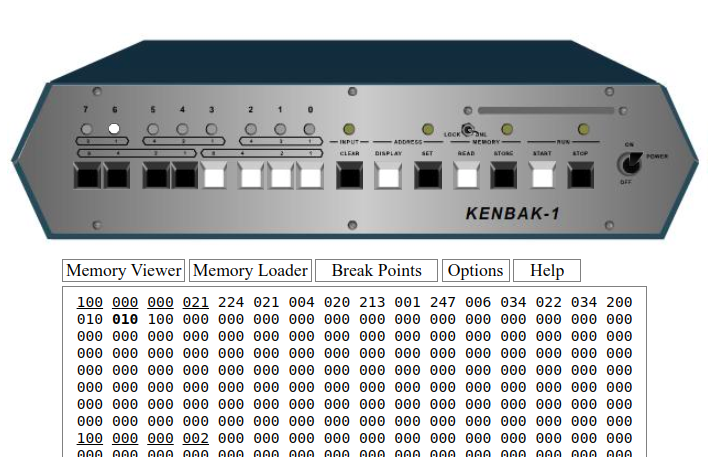
022: 000 Test the Project
I’ll paste this into the memory loader of the Kenbak-1 emulator. Then, I’ll hit start. I’m pre-loading cells 020, and 021 with the octal value of 010 (decimal 8). we get the octal value of 100 (which is decimal 64).
Summary of Kenbak-1 Multiplication
With the limited instruction of the Kenbak-1, we simply used addition to accomplish multiplication. Eight times eight just means that we add the number 8 to itself 8 times. Limited instruction sets allow us to do unlimited things. Sometimes, we just have to get a bit creative.
Octal Dump for Kenbakuino:
000,000,000,004,224,021,004,020,213,001,247,006,034,022,034,200,010,010,000,000,sFor more information, visit the Kenbak-1 Category Page!
— Ricky Bryce
