Introduction to Proportional, Integral, and Derivative (PID)
Proportional, Integral, and Derivative (PID) is a 3-step formula to bring a process to a setpoint, and attempt to hold it there. The example we will use is a heating process. We will bring fluid in a pipe up to a certain temperature and attempt to hold it at the setpoint. Other examples would include tank levels, flow control, and motor speeds.
Conceptual Example
Imagine the furnace at your house, which is controlled by a thermostat. This is NOT a PID because it simply turns on at one temperature, and shuts off at another temperature. Your house temperature is unstable using this method. Now, imagine if we had a special controller that controlled the amount of gas to the burners on your furnace.
The PID controller would decide exactly how much gas needs to be provided at all times. This would bring your house temperature up to the setpoint and hold it there. If you opened the door in your house, and the temperature started to drop, the PID would open the gas valve a little more. If the sun comes out for the day, the PID would detect that it needs to provide less output to maintain a constant temperature. Of course I’m just using your furnace example to help you understand the controller…. don’t try that at home!
Demonstration example
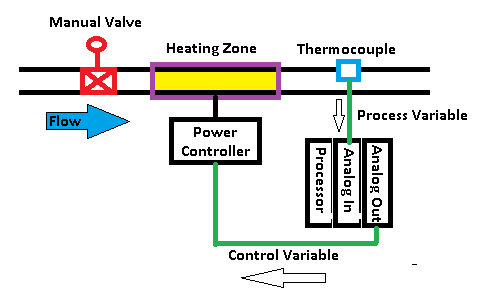
Compare that concept to the diagram below. If we open the manual valve, we will need to provide more output to maintain temperature of the fluid in the pipe. When you close the manual valve, we need less output.
Terminology
First, we will cover common terminology that you will need to know in order to understand the controller in this demonstration:
Control Variable: This is the output of the PID. In the above example, this is the output to the heating control unit.
Process Variable: This is the feedback from the system. In the above example, we have a thermocouple, or temperature transmitter. This allows you to see how the output is affecting the temperature.
Setpoint: In this demonstration, the setpoint is the temperature that we wish to acheive.
Error: Error is the difference between the setpoint and the process variable. This indicates how far away we are from the setpoint. The error can be positive, or negative depending on if our process variable is above or below the setpoint. Depending on the process, the error is calculated as the Setpoint minus Process Variable, or Process Variable minus Setpoint.
Proportional Overview
Proportional output is based on the amount of error. The more error we have, the more output will be affected. Let’s consider the following diagram:
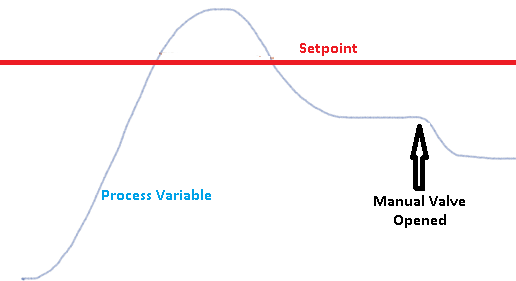
At the left of the graph, you will see that we have a lot of error. Our process variable is far from the setpoint. As the process variable approaches the setpoint, the error decreases. This means the output to our heat bands decrease. When the process variable is at the setpoint, we have no error, and therefore no output. However, it takes the heat bands a while to cool off, so we might see the process variable go above the setpoint. As the process variable comes back down, we still have no output until we are below the setpoint.
Problem using Proportional Only
In a heating system such as this, we will always loose heat from the system. This can be in the form of ambient losses, or losses due to load. When we constantly have losses, the process variable will not stay at the setpoint. With proportional output only (in this example), we must have error to provide enough output to make up for the losses.
Notice that our temperature (process variable) settles below the setpoint. When we open the manual valve, the fluid is taking more heat out of the system, so our error is greater. This will provide more output to make up for the losses. The temperature will naturally settle at a level that provides an exact output to make up for the losses. As you can see, the problem with only using proportional is that we cannot hold the process variable at the setpoint. Otherwise, we would have no output. It might work for a tank level if there are no leaks, but not in this heating process.
The tuning variable in the controller determines how much output we have based on each 1% of error.
Integral Overview
Next, we will discuss the Integral component of PID. Aside from the tuning variables, Integral is based on two components: Error and Time. Look at the following diagram:
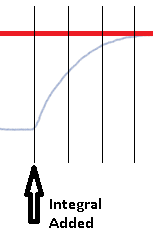
Here, we have our graph divided into 3 sections after integral is added. These three sections are time periods. Look at the error in the first time period We have quite a bit of error in this first time period, so quite a bit of output is provided. Look at the second (middle) time period. Although the same amount of time is passed in this time period, we have less error. Therefore, we ADD less to the output. We don’t decrease the output… We just have less to add to the output.
During the third time period, we have even less to add. We can say that as our process variable approaches the setpoint, we continuously add to the output, but just have less and less to add during each time period until we approach the setpoint. At the setpoint, we have nothing to add to the output, because there is no error.
The tuning variable for integral determines how often these time periods occur. Each time period is called a “repeat”. These repeats can be closer together (more aggressive), or further apart to make the Integral less aggressive.
Derivative Overview
Derivative is based on rate of change of error. This is used for “Anticipation”. Derivative is not used very often because it can cause problems if we have a noisy process variable. Derivative also complicates the tuning of your loop because changes in the other parameters affect the rate of change of error, and therefore affect your derivative. Let’s consider the following diagram.
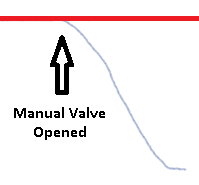
As soon as the valve is fully opened, our temperature starts to drop fast. In the few seconds after the valve is opened, we don’t have a lot of error. This means we do not have a lot of output based on Proportional. Also, not a lot of time has passed yet, so we don’t have much output based on Integral. We do have a large rate of change of error though. Derivative will provide output based on this rate of change of error. Derivative opposes a change in the process variable. Please be aware, though, that as the temperature starts to come back up to the setpoint later on, the slope is in the opposite direction. This means that as the process variable goes down, our output will be increased. As the process variable comes back up, the output is decreased!
The tuning variable for derivative determines how much our output is affected based on this rate of change of error.
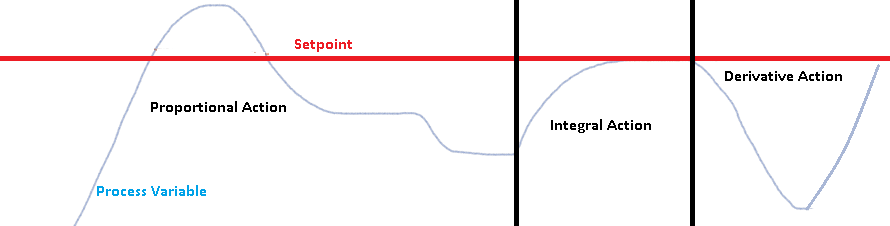
All Actions
Here we have a graph of the appearance of each separate component.
For more information on ControlLogix, please visit the ControlLogix Post page!
— Ricky Bryce
