Introduction to Kenbak-1 Division
We’ll need to come up with a creative way to do Kenbak-1 Division. The Kenbak-1 does not have a way to divide directly by using instructions. We’ll simply need to do the division manually.
Basically, the method I’ll use for this is to simply keep extracting the divisor from the dividend. We’ll see how many times we can subtract the divisor until we hit zero. What’s left will be the remainder.
Keep in mind that we are not doing floating point. Also, remember that the numbers in this post are all in octal.
You will probably want to print out a few copies of the Kenbak-1 Programming Worksheet. The worksheet itself is a great resource for understanding how to develop your commands. For this post, I’ll be using the Kenbak-1 Emulator. If you have a hardware emulator, I’ll paste the octal dump at the bottom of this post. You can send the octal dump to your hardware emulator, or enter it manually through the front panel.
Remember, our goal is for the user to enter the dividend into address 040, and the divisor into address 041. After the program runs, memory cell 050 will contain the answer. Likewise, cell 051 will contain the remainder. After that, the program simply stops.
Initialize the Registers for Kenbak-1 Division
First, we’ll set the A, B, and X registers to zero. At the same time, we’ll set the program counter to start at cell 004. We’ll be utilizing all three registers for this program. For now, we’ll also have the program initialize the values of these registers in case we ever need to jump back to this logic again.
REMEMBER ALL VALUES ARE IN OCTAL
THE ANSWER IS STORED TO 050 WITH THE REMAINDER IN 051
INIT:
000: 000 000 000 004
RESET:
004: 023 000 LDA 000
006: 123 000 LDB 000
010: 223 000 LDX 000Run the Calculation
At this point, we are ready to figure out how many times we can subtract register 041 from 040 before we hit zero. Basically, we need to load the A register with the dividend. After that, we’ll store the A register to the B register. The reason we are doing this is because of the final subtraction. At some point, we’ll perform a subtraction the results in a value less than zero. This means that whatever the value was before we performed the last subtraction is our remainder.
At cell 020, we jump to an area of memory that will increment X. We are testing “A” to see if it’s still greater than or equal to zero. If it is, we jump down to cell 030. After cell 030 increments X, it simply jumps back to cell 014.
LOAD:
012: 024 040 LDA 040 (LOAD DIVIDEND)
CALC:
014: 034 001 STA 001 (TEMPORARY STORAGE)
016: 014 041 SUB A 041 (A-[041])
020: 046 030 JPD A >= 0 030 (INCREMENT X)Store the Result
If the A register drops below zero, then we know it’s previous value (located in the B register) is the remainder. At this point, the value of X is our answer. We will store the answer to memory cell 050, and the remainder to cell 051.
ANSWER:
022: 234 050 STX 050 ANSWER
024: 134 051 STB 051 REMAINDER
026: 000 000 HALTIncrementing the X register for Kenbak-1 Division
Recall that earlier in our project, we had to jump down to cell 030 if the A register is still greater than zero. That way, we can increment the X register. We’ll do that here, then jump back up to cell 014 to start the next subtract operation.
INX:
030: 203 001 ADD X 001 (X=X+1)
032: 344 014 JPD CALCEnter Values and Test your Work
We’ll go ahead and make our dividend and the divisor part of our program. That way, we don’t have to manually enter the values from the front panel.
034: 000 000
036: 000 000
040: 100 003 You can paste this logic directly into the Kenbak-1 emulator’s memory loader. Here is the full code listing.
LOAD DIVIDEND TO 040 AND DIVISOR TO 041
REMEMBER ALL VALUES ARE IN OCTAL
THE ANSWER IS STORED TO 050 WITH THE REMAINDER IN 051
INIT:
000: 000 000 000 004
RESET:
004: 023 000 LDA 000
006: 123 000 LDB 000
010: 223 000 LDX 000
LOAD:
012: 024 040 LDA 040 (LOAD DIVIDEND)
CALC:
014: 034 001 STA 001 (TEMPORARY STORAGE)
016: 014 041 SUB A 041 (A-[041])
020: 046 030 JPD A >= 0 030
ANSWER:
022: 234 050 STX 050 ANSWER
024: 134 051 STB 051 REMAINDER
026: 000 000 HALT
INX:
030: 203 001 ADD X 001 (X=X+1)
032: 344 014 JPD CALC
034: 000 000
036: 000 000
040: 100 003
As you can see, our answer is 025 with a remainder of 001. Remember these tables are in OCTAL. You can check this against a programming calculator.
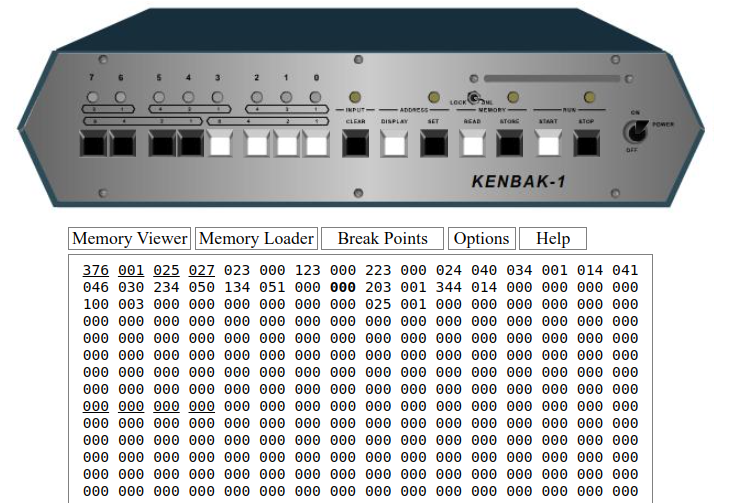
Kenbakuino Octal Dump
000,000,000,004,023,000,123,000,223,000,024,040,034,001,014,041,046,030,234,050,134,051,000,000,203,001,344,014,000,000,000,000,100,003,sTo test your answer on the Kenbakuino, just press stop, then clear. Enter 050 on the front panel buttons. Press SET. Now press READ, and you should see 025 (octal) on the display. Press READ again, and you will see the contents of cell 051. This is the remainder of 001.
For more information, visit the Kenbak-1 Category Page!
— Ricky Bryce
