Introduction to Calculating Resistance (Ohms)
In this section, we will be calculating Resistance in series and parallel circuits. A resistor is one of the most basic components of electrical circuits. The unit of resistance is called an Ohm. It’s purpose is to restrict the flow of electrons. To relate this to a mechanical example, just look at your faucet. When the faucet is completely shut, you have infinite resistance. When the faucet is completely open, you have nearly zero resistance to current flow. Resistors themselves have a fixed resistance, but if you need a variable resistor (like your faucet), you might use a potentiometer.
Working with resistors, and knowing how they interact with each other is a fundamental part of your knowledge of electricity. All electrical devices have some resistance, and if we know the value of resistance, and the voltage, we can calculate current flow (amps), so we know what size fuse to use in our circuit for protection.
Determining the Value
The easiest way to determine the value of a resistor is with an ohm meter. If you do not have an ohm meter, you can read the color bands on the resistor to determine it’s value. Let’s look at these resistors which are all the same value:

The problem with reading resistor values this way is that some colors are hard to tell apart, but in this case, the color bands read Blue, Violet, Red, and Gold. Refer to this chart to determine the resistance: Blue is the first band, so the first number in our value is 6. Violet is our second band, so then next number in our value is 7. The third band tells us how many zeros to add after this number, so since the band is red, we add two zeros. Our value is 6700, or 6.7 Kilo Ohms.
Value Color
0 Black
1 Brown Tolerance Band
2 Red Gold 5%
3 Orange Silver 10%
4 Yellow No Band 15%
5 Green
6 Blue
7 Violet
8 Gray
9 White
Here is an example of measuring a 10K resistor on an multimeter. A multimeter can measure a variety of parameters such as voltage, current, capacitance, and temperature depending on the meter that you purchase. You can see here that we are reading 9.77 Kilo Ohms which is within the specifications of 5% tolerance.

Calculating Resistance in Complex Circuits
By understanding how resistors interact with each other, you can understand how other electrical loads work, such as your electrical oven, your coffee pot, and your toaster. You will also understand why plugging too many items into the same circuit will blow your circuit breaker.
Calculating Resistance in Series

If you connect two resistors in series, this means that current flows through one resistor and then into the other. They are connected like train cars. To calculate the value of resistors in series, just add the values together. If we connect two 10K resistors in series, we should have 20K. Here we will test this on our meter.
So if we have 3 resistors (10K each) in series, we should have nearly 30K.

When checking the resistors with a meter, you will need to set the scale on your meter to a scale just above what you would expect to read. To read this value on my meter, I had to change the scale from 20K to 200K, because that was the next available scale on my meter. You will notice the higher the scale is on my meter, the less precision we have as far as decimal points.
Calculating Resistance in Parallel
Resistors in parallel are a little more difficult to calculate. Parallel means the resistors are connected on both ends, and current flows through both of them simultaneously. An example of a parallel circuit would be a light fixture in your house. The tips of the light bulb are both connected together, as well as the base. Connecting resistors in parallel DECREASES the resistance. A mechanical example of this would be turning your cold water on half way. Then when you also turn your hot water on half way, current will flow through both faucets simultaneously, therefore decreasing the resistance to flow.
The formula for calculating resistors in parallel is as follows:
1/R1 + 1/R2 + 1/R3 …… = 1/Rt
You just take 1 divided by each resistor individually to get a total. Your answer will be equal to 1 divided by the resistance value that you are attempting to find, so in short you add all of the reciprocals of the resistors together, then you will reciprocate the answer.
Let’s do an example of two 10K resistors in parallel:
1/10K + 1/10K = 1/Rt —-> 2/10K = 1/Rt —-> 10K/2 = Rt/1 —-> 5K=Rt
Our answer is 5K. Let’s test it on the meter.

OK. Now, let’s try three resistors in parallel:
1/10K + 1/10K + 1/10K = 1/Rt —-> 3/10K=1/Rt —-> 10K/3 = Rt/1 —-> 3.33333K = Rt
Again, let’s test this on the meter.

Now that we know how resistors work, we can use Ohms law to get the current flow. Here are some formulas for Ohms law where V is voltage, I is current (amps), and R is resistance.
V=IR —- I=V/R —- R=V/I
As long as we know two of the three variables, we can solve for the other. A resistor itself does not do anything in the real world other than to create heat, but remember, the resistor can be thought of as a stand-in for other loads such as your toaster at home (though it would be a much lower resistance, and therefore a lot more current flow).
Let’s calculate the current flow if I place 5v across the three resistors that we have in parallel. We know the resistance is 3.1K by our meter, even though we calculated 3.3K. This error is still within the tolerance of the resistor. To get the current, we will use the formula I=V/R –> I =5/3.1K –> I=0.001612903 Amps. This is 1.6 MilliAmps… so if we have a battery that is capable of producing 3500 mAh, the battery would supply the load for 2187.5 hours, or 91.15 Days.
Calculating Resistance in Series and Parallel Combination Circuits
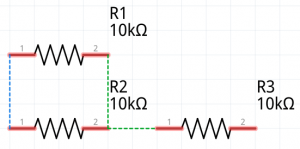
In the real world, your circuit will look more like this, because you will have a resistance in the wire itself before our power even gets to the load. Depending on the gauge of wiring you are using, you will have a certain amount of ohms per foot of cable. Let’s consider the following circuit that I built with Fritzing software.
It looks a little more complicated, but it’s still easy to calculate. First, we will figure out the resistive value of the parallel part of the circuit. R1 and R2 are both 10K, so we calculate 1/10K + 1/10K = 1/Rt —–> Rt = 10K/2 which is 5K. Since the value of the parallel branches are 5K, and it’s in series with the 10K, we just add the values together to get 15K.
If you are comfortable with understanding how resistors work, go to the next part of this lesson on calculating current!
If you would like industrial training at your facility for basic electric principles please visit my company’s website.
— Ricky Bryce
