Introduction to Marsenne Primes
Prime numbers are numbers that are only divisible by 1, and themselves of course. Prime numbers (perfect numbers) are important for encryption, and very interesting to math enthusiasts who love to study their patterns. Obviously, with large numbers, prime numbers become more rare.
An understanding of Marsenne primes depends heavily on your understanding of the binary numbering system. If you are unfamiliar with the binary numbering system, please check out my post on this here.
Understanding a Marsenne Prime
There are many posts on how Marsenne primes work. Most of them are very confusing and involve complex math. I will explain this to you in a way that I understand it. I’m a simple man, so I hope I can explain it in a way that you can understand this too as long as you understand how binary works.
Simply put, a Marsenne prime is a prime number that is one less than any number to the power of 2.
Any number in binary that is one less than the power of 2 has a certain number of bits that are set (1) in a row.
We will start with 4. One less than that is 3. This is a prime number, and 2 bits in a row (11) makes it a Marsenne prime.
Double Marsenne Primes
A double Marsenne prime is simple. In the example above, we know that 3 is one less than 2 to the power of 2. That gave us the value of 3. In binary that is 11.
Let’s carry that one step further. We know that 3 is a Marsenne prime. A double Marsenne prime means that we take the value of a Marsenne (or other) prime number, and put that many bits in a row. If the resulting number is a prime, we call that a double Marseene prime.
In this case, 3 is a prime number, so we put 3 bits in a row… 111 in binary, which is 7 in decimal. Since 7 is a prime number, we call this a double Marsenne prime.
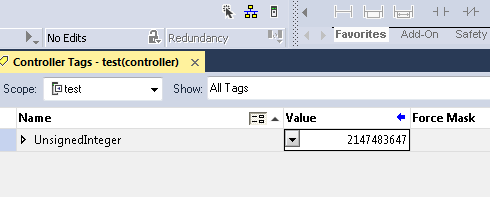
32 bit signed integer
In the ControlLogix processor (and other 32 bit processors) The number 2147483647 is very important to us. That is the maximum value that we can have for a timer or counter, or any other double integer.
Here is the reason that 2147483647 is a double prime: If we take the number 5, which is a prime number, and put 5 bits in a row, we have 31. Then if we put 31 bits in a row, we have 2147483647.
I do not recommend setting the preset of a timer to this number though. Depending on your scan time, the timer could overrun causing a processor fault!
Special thanks to a student in class, Casey who searched this number. He mentioned that this was a perfect number, and then I started researching this.
For more information on ControlLogix, check out the ControlLogix category!
–Ricky Bryce
