Introduction to Derivative Settings for ControlLogix PID Enhanced (PIDE)
Basically, the derivative settings for ControlLogix PID Enhanced will multiply the effect that derivative has in your closed loop system. We use derivative to anticipate, or predict error in the future. Consider this example:
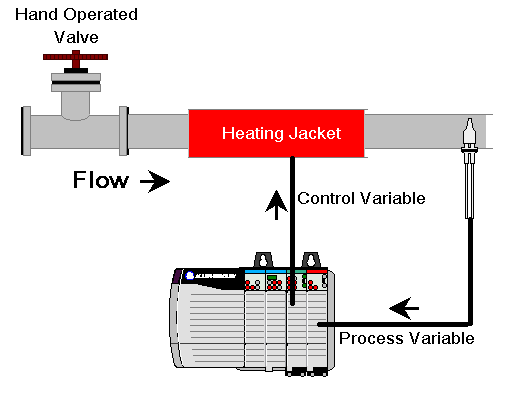
Obviously when you open the valve, a lot of fluid will flow through this system. This will cause the temperature to drop very quickly. At this point, the temperature has not dropped enough for the proportional gain to have much effect. In the same fashion, not enough time has passed for integral to have much effect. This is where derivative action is helpful in some scenarios. Derivative is based on the rate of change of error. Likewise, think of it as the slope. The steeper the decline in temperature, the more effect derivative will have.
Many processes have a noisy process variable (feedback). For this reason, derivative is seldom used. Also, controlling a loop is more simple when the technician only has to consider proportional and integral.
Another way to think of derivative is that it opposes a change in the process variable. In a heating system such as this, if the temperature drops, derivative will increase the output. Likewise if the temperature increases, derivative action will lower the output.
Derivative Settings for ControlLogix PID in our online process
At this time, let’s calculate what a good starting point for derivative should be. We learned that when we set the proportional gain, the natural period was about 5 minutes. This was when the loop became unstable. We also know that our PID is running independent mode reverse acting. We’ll set the derivative gain to the proportional gain times one eighth of the natural period. In this case, this would be 1.5 * .0625. This gives us a gain setting of 0.94.
With the Proportional gain at 1.5, integral gain at 3, and derivative set to 0.94, let’s see how the loop reacts. The process variable is red on the graph. The set point is green.
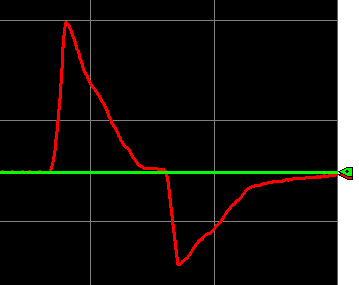
We have a fairly good response. On the left side of the graph, when we close the valve, the temperature spikes. The temperature comes right back to the set point. Likewise, when we open the valve, the temperature drops. The controller provides a lot of output to bring the temperature back up.
Experiments
Let’s try some other settings to get a “feel” for what the derivative action looks like. Here is a derivative setting of 3. Keep in mind the recommended setting is 0.94.
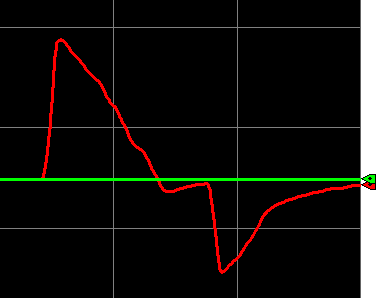
As you can see, the process variable is more spread out. The derivative is opposing the change in the process variable.
Once again, let’s take a look at what our graph looked like without derivative action. This graph is proportional and integral only.
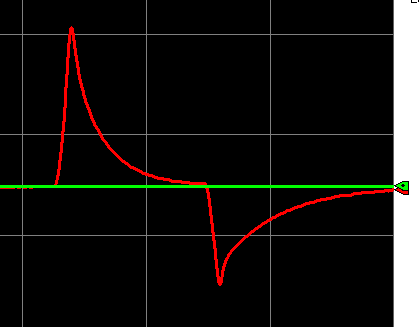
As you can see, the spike in temperature is greater, and you are back to the classic asymptotic curve of the integral action.
Summary
To summarize, derivative action works on change of error. This helps to minimize the spikes in temperature, and slows down the changes in the process variable.
If you have not done so yet, check out the documentation on Proportional, and Integral!
— Ricky Bryce
